弱化版:。
令\(f[x][i]\)表示\(x\)的子树中深度为\(i\)的点的个数,\(g[x][i]\)表示\(x\)子树中,满足\(u,v\)到\(LCA(u,v)\)的距离都是\(d\),且到\(x\)的距离为\(d-i\)的点对\((u,v)\)个数。(就是不以\(x\)作为三个点的中心位置,那样就没法算了)
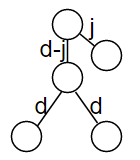
那么就可以由\(g[x][i]\)与另一棵子树的\(f[y][i-1]\),以及\(g[x][0]\)更新答案。
\(f\)的转移简单。\(g[x][i]\)要么是从某个子树中得到(\(g[x][i]+=g[v][i+1]\)),要么是以x作为LCA从某两个子树中得到(\(g[x][i]+=f[x][i]*f[v][i-1]\))。
直接这样复杂度\(O(n^2)\)。DP数组的下标都是深度,所以可以用长链剖分。继承重儿子时\(f\)需要右移,\(g\)需要左移,还是用指针方便些吧(\(g\)的前后都需要留空间)。
复杂度\(O(n)\)。为啥洛谷上跑的不快啊(30ms)==没道理啊。
//7788kb 376ms#include#include #include //#define gc() getchar()#define MAXIN 300000#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)typedef long long LL;const int N=1e5+5;int Enum,H[N],nxt[N<<1],to[N<<1],dep[N],mxd[N],son[N],pos[N],*f[N],Fp[N],*fp=Fp;LL Ans,*g[N],Gp[N<<1],*gp=Gp;char IN[MAXIN],*SS=IN,*TT=IN;inline int read(){ int now=0;register char c=gc(); for(;!isdigit(c);c=gc()); for(;isdigit(c);now=now*10+c-'0',c=gc()); return now;}inline void AE(int u,int v){ to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum; to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;}inline void Allot(int x){ f[x]=fp, fp+=mxd[x], gp+=mxd[x], g[x]=gp, gp+=mxd[x];}void DFS1(int x,int fa){ int mx=0; for(int i=H[x],v; i; i=nxt[i]) if((v=to[i])!=fa) dep[v]=dep[x]+1, DFS1(v,x), mxd[v]>mx&&(mx=mxd[v],son[x]=v); mxd[x]=mx+1;// for(int i=H[x],v; i; i=nxt[i])// if((v=to[i])!=fa) dep[v]=dep[x]+1, DFS1(v,x), mxd[v]>mxd[son[x]]&&(son[x]=v);// mxd[x]=mxd[son[x]]+1;}void DFS2(int x,int fa){ if(son[x]) f[son[x]]=f[x]+1, g[son[x]]=g[x]-1, DFS2(son[x],x); f[x][0]=1, Ans+=g[x][0];//重儿子子树与x的贡献 for(int i=H[x],v; i; i=nxt[i]) if((v=to[i])!=fa&&v!=son[x]) { Allot(v), DFS2(v,x); int l=mxd[v]; for(int j=1; j<=l; ++j) Ans+=g[x][j]*f[v][j-1]+g[v][j]*f[x][j-1]; for(int j=1; j<=l; ++j) g[x][j]+=g[v][j+1]+1ll*f[x][j]*f[v][j-1],f[x][j]+=f[v][j-1];//g[x][0]转移来也没啥用啊 }}int main(){ int n=read(); for(int i=1; i